Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Reprise du message précédent:
Tassle -
posté le 20/08/2019 à 22:43:01 (5274 messages postés)
| Disciple de Pythagolf | mamie : Bien ouej !
Si on utilise le vocabulaire de la théorie des graphes, tu viens de démontrer que les deux graphes représentés ne sont pas isomorphes, grâce à un passage au complémentaire !
Je pense qu'observer le complémentaire est effectivement ce qu'il y a de mieux dans ce cas, mais il y a d'autres méthodes, par exemple :
- On choisit une personne et on la supprime ainsi que tous ses ennemis (qui a dit kamikaze ?). Dans un cas, il y a une personne qui est amie avec toutes les autres personnes restantes, dans l'autre cas non.
- On peut aussi observer deux ennemis et garder uniquement les amis qu'ils ont en commun (on supprime les deux ennemis également). Dans un cas ça fait une petite chaine de l’amitié, dans l'autre cas ça donne deux couples.
- Et sans doutes beaucoup d'autres.
|
~~ |
Suite du sujet:
Tassle -
posté le 22/08/2019 à 18:43:27 (5274 messages postés)
| Disciple de Pythagolf | Je continue avec mes énigmes pour faire chier les gens qui aiment pas les maths  (j'essaye quand même de trouver des trucs qui ressemblent pas tellement à des maths vu de loin)
Vous vous apprêtez à faire un voyage sur le continent Q, composé de 5 pays. Pour pouvoir vous la péter sur instabook, vous aimeriez traverser toutes les frontières possibles entre deux pays du continent. Le souci, c'est que vous transportez constamment avec vous votre stock de drogues illégales, espèce de junkie. Vous aimeriez donc minimiser les risques et traverser chaque frontière une seule et unique fois.
1er scénario (représenté à gauche) :
Vous est-il possible de planifier votre trajet pour traverser chaque frontière entre pays limitrophes une seule et unique fois ? Vous pouvez commencer dans n'importe quel pays de Q et finir dans n'importe quel pays de Q. Pas le droit de prendre l'avion, de sortir du continent en cours de route ou d'essayer de traverser deux frontières à la fois en passant par un point où trois pays se touchent (ou autres astuces bizarres auxquelles j'ai pas pensé).
2nd scénario (représenté à droite) :
Pour collecter encore plus de likes vous aimeriez aussi inclure toutes les frontières avec les eaux internationales dans votre trajet. Vous pouvez commencer et/ou finir dans les eaux internationales si ça vous chante. Même restrictions qu'avant, sauf qu'évidement vous pouvez maintenant sortir du continent (mais uniquement par bateau). Est-ce possible ?
|
~~ |
François Berhn -
posté le 22/08/2019 à 18:59:44 (5402 messages postés)
| Tonton Hellper | Pour le 1 je dirais que c'est possible en commençant sur le vert et en finissant sur le orange ou vice versa mais j'ai la flemme de le prouver
Et je crois que 2 un impossible.
|
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux |
Tassle -
posté le 23/08/2019 à 17:13:40 (5274 messages postés)
| Disciple de Pythagolf | Le premier est bien possible pourtant, comme tu l'as montré, donc la réponse est pas toujours non 
(bien ouej)
|
~~ |
|
| Chanter l'hyperchleuasme | Pas mal. Je vais piquer ça pour mon jeu 
EDIT : voilà !
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tassle -
posté le 24/08/2019 à 00:13:58 (5274 messages postés)
| Disciple de Pythagolf | La théorie des graphes est un bonne source d'énigmes 
Vous avez fait la découverte d'un ancien manuscrit qui vous a mené à une grotte possédant deux embranchements qui se rejoignent à une porte magique.
Vous apprenez dans le manuscrit que celle-ci s'ouvre lorsque vous prononcez à voix haute "Abricotier" et que dès que l'on s'éloigne de plus d'un demi-pas de la porte, celle-ci se referme. Et effectivement cela fonctionne. Vous en êtes très heureux et voudriez partager cela avec l'archéologue du coin, Benjamin Jones. Cependant, vous ne voulez pas lui révéler le mot magique par peur qu'il s'accapare votre découverte et les louanges de la communauté archéologique avec. Vous ne voulez pas non-plus qu'il puisse voir la porte ouverte, car à l'intérieur du cadre se trouve inscrit "Abricotier" de manière très visible.
Pouvez-vous le convaincre que vous connaissez bien ce mot magique sans lui révéler ? Ici convaincre signifie que Benjamin Jones est quasiment certain que vous connaissez bien ce mot, à 99,9% par exemple.
Informations supplémentaires sur la grotte:
- Il y a beaucoup de résonance dans cette grotte. Cela veut dire Benjamin Jones ne peut pas se trouver à l'intérieur au moment où vous ouvrez la porte, car il entendrait le mot magique. Mais cela veut aussi dire que vous l'entendriez rentrer si il voulait le faire en douce (et que vous pouvez le localiser approximativement dans le grotte, au son).
- L'embranchement ne se voit pas depuis l'entrée de la grotte.
- La porte ne se voit pas depuis l'embranchement.
- Aucun appareil électronique ne fonctionne à l'intérieur, il est impossible d'utiliser un GPS par exemple pour montrer que vous avez bien fait le tour de la grotte. (Et de manière générale, une solution valide ne doit faire usage d'aucun outil)
Edit: - La porte laisse passer le son, de manière ce que que Benjamin Jones ne puisse pas se dire "Tiens le son vient avec la même intensité des passages gauche et droite donc la porte doit être ouverte".
(L'énigme est pas de moi, c'est adapté d'un truc qui est pas posé sous forme d'énigme d'habitude. J'en dis pas plus pour l'instant pas que vous googliez la réponse.)
Edit: Ahh je viens de voir sur la première page que ce topic est censé fonctionner comme celui du jeu "Qu'est-ce que c'est". Donc euh désolé. mamie si tu veux proposer une énigme je jarte celle-ci et je la garde pour quand j'aurai la main :V
|
~~ |
Tassle -
posté le 24/08/2019 à 01:47:44 (5274 messages postés)
| Disciple de Pythagolf | Ahlala, faut que je rajoute que la porte ne fait pas de bruit alors (ou que Benjamin Jones ne peut pas savoir si t'es très fort en imitation de bruits de portes, donc tu pourras pas le convaincre à 99,9%)
|
~~ |
|
| Narrer l'autocatégorème | Je lui demande de placer un objet près d'un côté de la porte et un autre de l'autre côté, puis on se place à l'entrée et il chronomètre combien de temps je mets, en partant de l'entrée, pour ramasser les deux objets puis pour revenir à l'entrée. Si j'ai bien la capacité d'ouvrir la porte j'aurai un chrono infaisable autrement.
|
Quel RPG Maker choisir ? • Ocarina of Time PC • Polaris 03 |
NeoSephiroth -
posté le 24/08/2019 à 10:30:32 (3718 messages postés)
-  | Neo_Sephiroth | Je lui demande de d'abord venir voir que la porte est bien fermé, puis je le fais ressortir pour 1min.
Pendant qu'il est dehors, j'ouvre la porte.
1min plus tard il entre dans la grotte et se place à l'embranchement.
Par le son de ma voix, il sait que je suis coté A de l'embranchement.
Je traverse la porte, par le bruit de mes pas il entends que j'arrive depuis le coté B et me voit effectivement revenir depuis le coté B.
Non ?
(ps d'outil nemau, sinon perso j'avais pensé à laisser un truc, genre un tshirt, traverser la porte fermer, en le plaçant dans le cadre avant la fermeture.)
|
Tassle -
posté le 24/08/2019 à 12:41:16 (5274 messages postés)
| Disciple de Pythagolf | Nemau > Effectivement, pas d'outils ^^
NS > Pas mal, mais on ne peut localiser qu'approximativement quelqu'un dans la grotte et tu ne peux pas t'éloigner de la porte sans que celle-ci se referme, donc il saura juste que t'es près de la porte.
Juste pour prévenir un autre facteur auquel j'avais pas pensé : La porte laisse passer le son, de manière ce que que Benjamin Jones ne puisse pas se dire "Tiens le son vient avec la même intensité des passages gauche et droite donc la porte doit être ouverte".
Désolé de rajouter des restrictions comme ça, mais j'attends une solution précise (ou quelque chose qui s'en rapproche assez). Quand j'ai dit "99.9%" c'était pas pour rien. Mais pour vous aider et vous mettre sur la piste j'autorise également une solution convaincante à 75%, c'est à dire une solution où à la fin Benjamin Jones se dit "il n'y a que 25% de chances que ce que je viens de voir/vivre/whatever" se produise si ce mec ne connait pas la formule magique.
|
~~ |
|
| Chanter l'hyperchleuasme | On montre une première fois la porte à Benjamin Gates pour qu'il constate qu'on ne peut pas l'ouvrir.
On fait sortir Benjamin Gates de la grotte.
On dit à Benjamin Gates de compter jusqu'à 100 puis de rentrer dans la grotte.
Pendant qu'il compte à l'extérieur, on ouvre la porte et on attend au niveau de la porte.
Arrivé au croisement, Benjamin Gates doit nous demander de le rejoindre soit par la gauche soit par la droite, selon son choix.
Comme la porte est ouverte, on peut arriver par le chemin que Benjamin Gates aura décidé.
Répéter l'expérience 1000 fois, et Benjamin Gates sera sûr et certain qu'on peut ouvrir la porte.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tassle -
posté le 24/08/2019 à 13:13:16 (5274 messages postés)
| Disciple de Pythagolf | Bien joué Et pour arriver à 99,9% de certitude, 10 répétitions suffisent (la probabilité de réussir 10 fois de suite sans connaître le secret est de (1/2)^10 < 0.0001 = 0.01%)
L'énigme (qui n'est pas une énigme à la base) vient d'un article de Guillou et Quisquater (deux chercheurs en crypto) intitulé "How to explain zero-knowledge protocols to your children" et qui parle de Preuves à divulgation nulle de connaissance (ou Zero-Knowledge Proofs, ZKP, c'est plus concis en anglais). L'article Wikipédia parle de l'exemple de la grotte.
Les ZKP sont un concept très important en cypto moderne. Le principe général c'est qu'on veut prouver une proposition P à quelqu'un mais sans lui donner plus d'information sur cette proposition ou comment il pourrait lui même la prouver à quelqu'un d'autre. Souvent ces propositions sont sous la forme "je connais x tel que machin" (ici, je connais le secret qui ouvre la porte) et vous voulez convaincre votre interlocuteur sans révéler la moindre information sur x (autre que "x existe et je le connais" évidemment).
Ça permet plein de trucs cools et ça peut s'appliquer à des domaines super variés. Par exemple, dans une précédente énigme j'ai demandé si deux graphes (deux "réseaux d'amis") étaient isomorphes ("peuvent représenter le même groupe d'amis"). Et bien sur des gros graphes ce problème est très dur à résoudre en pratique (en théorie on sait pas trop). Mais on peut prouver à quelqu'un qu'on connaît le moyen de passer d'un graphe à l'autre en renommant les sommets sans rien lui apprendre sur la façon de renommer les sommets. Ou au contraire prouver qu'ils ne sont pas isomorphes sans que la personne puisse utiliser cette connaissance pour à son tour prouver qu'ils ne le sont pas.
Voilà j'ai un oral sur les protocoles cryptographiques dans deux jours et plutôt que réviser je me suis dit que faire des énigmes c'est plus sympa
|
~~ |
AzRa -
posté le 24/08/2019 à 13:25:36 (11278 messages postés)
| 418. I'm a teapot. | Ah oui j'ai entendu parler du zero-knowledge. Ca sert à faire des shitcoins aussi. Genre zcash.
|
Agus fagaimid suid mar ata se. |
Verehn -
posté le 24/08/2019 à 20:11:46 (9058 messages postés)
-  | Vhehrhehn | Avant de lire la réponse de RotS j'avais une solution bidon et bourrine réfléchie en 2min: à l'aide d'un gant de protection placer un oursin très dense (manufacturé pour être particulièrement dangereux, s'il le faut), à moitié peint en blanc, à côté de la porte => celui qui connait le mot de passe se met tout nu => vérifier X fois que l'oursin a bougé après avoir été frappé par la porte, le replacer à chaque fois, et vérifier que le corps du mec tout nu n'est pas blessé d'avoir tenté X fois de le déplacer.
Ouais, c'est vraiment pas le genre de solution qu'on recherche.
(Edit: et faudrait vider la grotte de tout caillou/outil permettant de frapper l'oursin.  )
Intéressant ces histoires de preuves à divulgation nulle.
|
Eldrao ~ PakuPaku ~ Winged Light ~ Ruin ~ Ma galerie ~ LTDAD ~ Don de graphismes plateforme 2D |
Tassle -
posté le 24/08/2019 à 23:27:13 (5274 messages postés)
| Disciple de Pythagolf | Effectivement c'était pas le genre de solution attendu
Ouais c'est intéressant, du coup j'aurais dû écouter le cours pendant le semestre, là je sens que je vais juste me ramasser à mon oral =>[]
J'avais pas vu ton edit pour l'énigme de Kujira RotS, c'est sympa Est-ce que le fait qu'on ne puisse sortir que par la droite ça divulgue pas déjà l'endroit où on doit finir ?
D'ailleurs la main est à toi.
|
~~ |
|
| Chanter l'hyperchleuasme | Euh ça divulgue un peu, mais celui qui comprend ça mérite l'info.
Énigme des lunes
Une grille de 4*4 = 16 cases.
Chaque côté de case est soit rentrant, soit sortant.
Dans l'exemple au milieu, j'ai tracé en jaune des côtés sortants et rentrants.
Les cases ont donc diverses formes : pleine lune, croissant de lune vers le bas, vers le haut... diabolo horizontal, diabolo vertical, forme d'éventail orientée vers haut-gauche, vers bas-droite... et une étoile.
J'ai listé les 16 formes possibles de cases tout en bas.
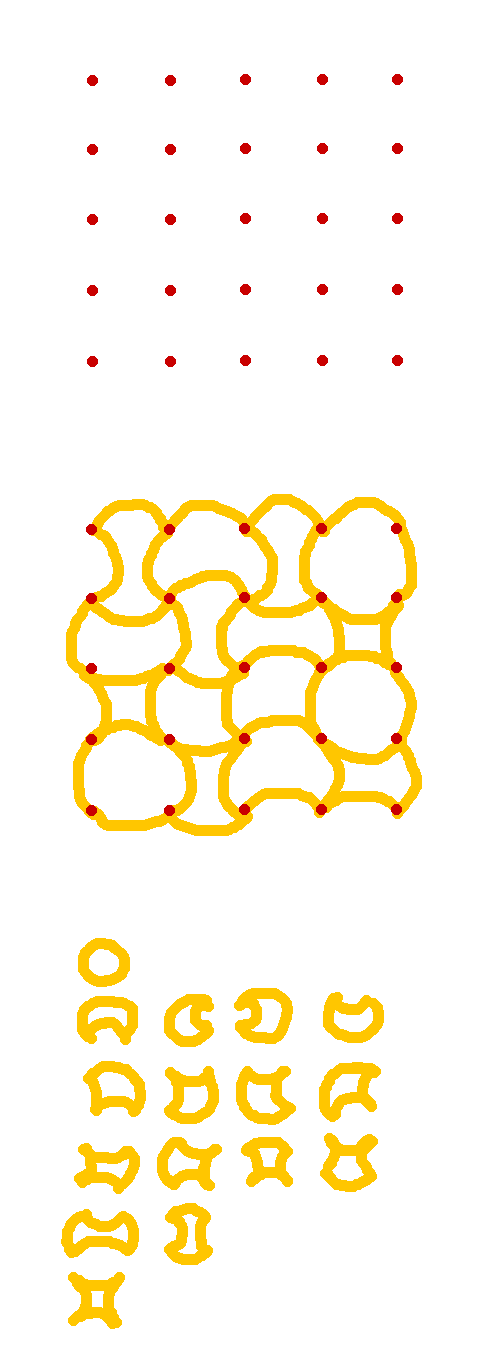
La grille que j'ai complétée n'est pas bonne, parce que :
- premièrement elle ne comporte pas les 16 formes de cases possibles
- et deuxièmement elle n'est pas pavante, puisqu'en haut il y a un côté sortant alors qu'en bas il y a un côté sortant également (ça ne s’emboîterait pas).
La question : est-il possible de dessiner la grille avec les 16 différents types de case présents une fois chacun, et que la grille résultante soit pavante ?
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tassle -
posté le 25/08/2019 à 01:25:12 (5274 messages postés)
| Disciple de Pythagolf | 
Plutôt étonné que ça soit possible, j'ai passé 10 minutes à tenter de trouver un invariant qui rendait ça impossible avant d'essayer :V
|
~~ |
|
| Chanter l'hyperchleuasme | Très bien.
Cette solution est irrégulière, pour info il y en a d’autres, plus symétriques.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tassle -
posté le 25/08/2019 à 12:40:25 (5274 messages postés)
| Disciple de Pythagolf | En essayant de régulariser ma solution j'obtiens ça:
Spoiler (cliquez pour afficher)
|
~~ |
AzRa -
posté le 25/08/2019 à 12:52:21 (11278 messages postés)
| 418. I'm a teapot. | Vraiment superbe, oui, surtout quand on connait la particularité du truc.
|
Agus fagaimid suid mar ata se. |
Tassle -
posté le 25/08/2019 à 17:19:55 (5274 messages postés)
| Disciple de Pythagolf | Dans la même veine que mon énigme précédente:
Votre ami Victor possède pas mal de cadenas à combinaisons pour vélos de ce type là :
Si il vous en présente deux, il est facile de lui démontrer que vous connaissez le code d'au moins un des deux sans qu'il sache lequel :
- Il vous donne les deux cadenas fermés, vous vous cachez pour ouvrir celui dont vous connaissez le code et le refermer sur l'autre cadenas. Puis vous présentez à Vic les deux cadenas attachés l'un à l'autre.
(on va négliger la probabilité que vous ayez juste deviné un code, d'autant que la distinction entre "connaître un code" et "savoir deviner un code" est pas forcément super claire si on commence à tout formaliser)
Maintenant, plus compliqué :
Victor vous présente un certain nombre de cadenas, disons 10, et vous voulez lui prouver que vous savez en ouvrir au moins deux d'entre-eux, sans révéler plus d'info que cela. (Victor ne doit pas pouvoir deviner lesquels, ni en exclure certains, etc).
Comment faire ?
EDIT :
INFO IMPORTANTE OUBLIÉE : Victor sait tous les ouvrir.
|
~~ |
AzRa -
posté le 25/08/2019 à 17:36:57 (11278 messages postés)
| 418. I'm a teapot. | Tu te caches pour ouvrir les deux cadenas et tu les lui ramène ouverts, avec les 8 autres fermés.
C'est peut-être moi qui ai mal chopé un détail mais je pense qu'il manque quelque chose dans ton énoncé. Mais ça a pas l'air d'être une énigme, ça.
EDIT : Ok je pense que j'ai compris. Tous les cadenas sont différents et on peut le voir d'un coup d'oeil. Genre ils ont tous des couleurs différentes. (De but en blanc je me les étais imaginés identiques). Ok je cherche la réponse.
|
Agus fagaimid suid mar ata se. |
Tassle -
posté le 25/08/2019 à 17:42:32 (5274 messages postés)
| Disciple de Pythagolf | Ahhh j'avais pas vu qu'on pouvait le comprendre comme ça.
Quand je dis "sans révéler lesquels" je sous-entendais que tous les cadenas sont différenciables, tu peux pas simplement les mélanger dans un sac et à la fin tu sais plus lequel est lequel.
Disons que chaque cadenas a une couleur différente.
Donc là tu lui révèles carrément lesquels tu sais ouvrir.
(Et je veux pas d'histoire de "je les repeins tous de la même couleur" ou autre filouteries du genre )
Edit: Yep, grilled.
|
~~ |
NeoSephiroth -
posté le 25/08/2019 à 18:30:32 (3718 messages postés)
- | Neo_Sephiroth | Citation: vous voulez lui prouver que vous savez en ouvrir au moins deux d'entre-eux |
On sait en ouvrir plus que deux ?
Faut t-il qu'il pense qu'on ne peut en ouvrir au maximum que deux ?
Parce qu'on peut remplir l'affirmation "au moins deux" en formant formant un chaine refermé sur elle meme en cercle.
Ca veut simplement dire qu'on sait en ouvrir certains, plus que 2 mais il saura pas lesquels.
|
Tassle -
posté le 25/08/2019 à 19:04:36 (5274 messages postés)
| Disciple de Pythagolf | On sait en ouvrir au moins deux. Peut-être plus, peut-être pas. Mais on peut toujours se ramener au cas où on sait en ouvrir exactement deux en "oubliant" les autres codes (en se forçant à pas les utiliser quoi). Donc partons du principe qu'on sait en ouvrir exactement deux.
Victor à la fin doit quand même se dire "il sait en ouvrir au moins deux" (parce que même si on savait tous les ouvrir on pourrait se contenter de faire comme si c'était pas le cas, donc on pourra jamais convaincre Victor qu'on ne sait pas tous les ouvrir).
Je vois pas quelle tronche elle a ta chaine, tu peux préciser ?
|
~~ | Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27Index du forum > La Taverne > Topic des énigmes BDM
|
Chat
- 
