Bienvenue
visiteur !

Index du forum > La Taverne > Topic des énigmes BDM

Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

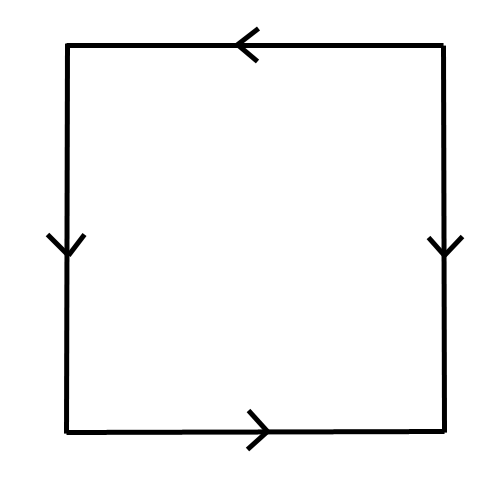
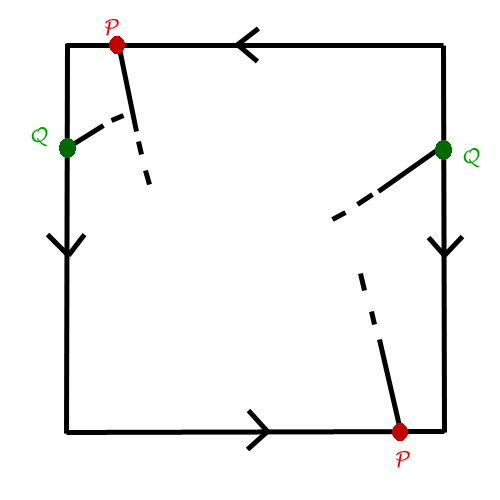
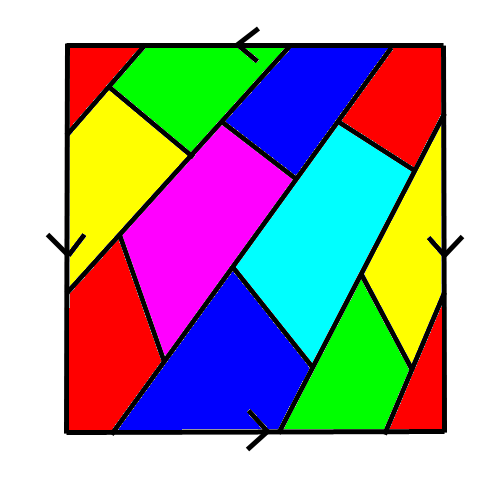
Reprise du message précédent:

Roi of the Suisse - posté le 15/06/2013 à 18:33:50 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Alors voici la carte d'une planète : La carte "boucle". Les côtés gauche et droit se touchent, les côtés haut et bas se touchent. Cependant, les côtés gauche et droit se touchent dans le même sens, alors que les côtés haut et bas se touchent dans le sens contraire (par exemple si sur le côté haut un point est près du bord gauche, en bas il sera prêt du bord droit. Sur cette planète il y a plein de pays délimités par des frontières, la frontière se prolonge d'un côté à l'autre du carré (en symétrie axiale verticale pour les côtés verticaux, en symétrie centrale pour les côtés horizontaux, comme expliqué précédemment). Pour que la carte soit jolie, on colorie les pays qui se touchent avec des couleurs différentes : (ici chacun des 5 pays touche les 4 autres, donc il faut 5 couleurs minimum) (ici les deux pays jaunes ne se touchent pas : on peut utiliser la même couleur) (on remarque d'ailleurs l'inversion de l'ordre des couleurs entre le côté haut et le côté bas du carré) Voici la même carte coloriée avec plus de couleurs qu'il n'en suffisait : Cette solution n'est pas optimisée. Donc il faut bien vérifier en ajoutant une nouvelle couleur qu'on ne pouvait pas faire autrement ! Quel est le plus petit nombre de couleurs qui permet de colorier TOUTES les cartes possibles sur cette planète ? Donner une carte qui illustre ce cas extrême. De préférence une carte la simple possible : avec autant de pays que de couleurs.
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Suite du sujet:

Tasslehoff - posté le 15/06/2013 à 19:25:30 (5274 messages postés) ❤ 0
Disciple de Pythagolf	Le nombre de pays importe ?
~~

Roi of the Suisse - posté le 15/06/2013 à 19:32:31 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Il y a un nombre de couleurs fixe qui permet de colorier toutes les cartes possibles sur cette planète. Quelque soit le nombre de pays, il y aura toujours le même nombre plafond de couleurs à utiliser. Si le maximum est 11 couleurs, quelque soit le nombre de pays (même 8000), 11 couleurs suffiront toujours.
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

criket - posté le 15/06/2013 à 19:34:58 (1389 messages postés) ❤ 0
LesFiersAuxCrabes ftw	Je suppose que le résultat trouvé par recherche internet n'est pas valable
Que fera le passé ? Rien. Que fera le futur ? Tout. Rejoignez le parti du futur !

Tasslehoff - posté le 15/06/2013 à 19:35:26 (5274 messages postés) ❤ 0
Disciple de Pythagolf	Bah non, pas si il y a 2 pays, ça devient un majorant.
~~

Hellper - posté le 15/06/2013 à 19:37:16 (5402 messages postés) ❤ 0
Tonton Hellper	Sauf que tu ne peux pas avoir que deux pays je pense.
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux

Kisthune - posté le 15/06/2013 à 20:01:57 (1227 messages postés) ❤ 0
Oui c'est fait à l'arrache	Question bête, mais tu peux avoir de pays scindés en morceaux (= espace non connexe) ?
Reikon no Yume

Roi of the Suisse - posté le 15/06/2013 à 20:36:48 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Tass et Hellper : Il y a des cas où 1 2 3 4 5 couleurs suffisent, j'ai moi-même donné un exemple à 5 couleurs. Mais si le maximum est 18, il n'y a pas de carte qui nécessite 19 couleurs. Il y a des cartes qui demandent moins, certes, mais jamais plus que le maximum général. Quiche : les pays sont connexes ! et par des arêtes, pas par des sommets
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Hellper - posté le 15/06/2013 à 21:32:58 (5402 messages postés) ❤ 0
Tonton Hellper	Donc il faut démontrer que c'est possible d'avoir 6 couleurs sans couleur inutile. Si ça marche pas c'est que le maximum est 5 et si ça marche il faut refaire la manip pour 7.
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux

Roi of the Suisse - posté le 15/06/2013 à 21:35:53 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Voilà.
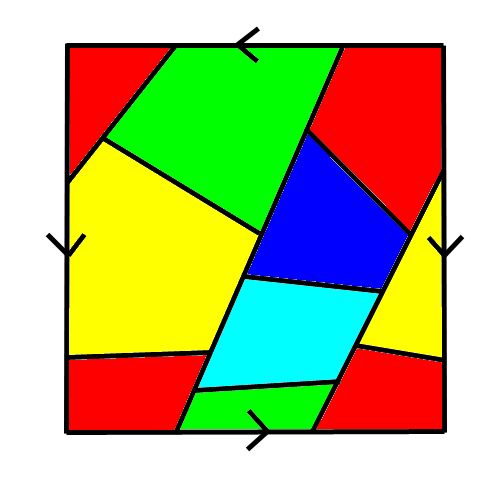
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Hellper - posté le 15/06/2013 à 21:41:51 (5402 messages postés) ❤ 0
Tonton Hellper	C'est possible avec 6. Voilà la preuve : Je pense même que 6 est le maximum car si on rajoute une zone qui est en contact avec les 6 autres, on sépare la zone d'une de ses zones adjacentes et le rose devient alors obsolète. Voici une image pour appuyer mon propos : La nouvelle zone coupe la précédente du jaune et du vert. Dou coup on peut mettre la nouvelle zone en rose et l'autre on peut la changer en jaune
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux

Tasslehoff - posté le 15/06/2013 à 21:43:32 (5274 messages postés) ❤ 0
Disciple de Pythagolf	Il faut le prouver ou juste le conjecturer ? Parce que le prouver ça me parait chaud... (rien que de conjecturer je vois pas de suite là)
~~

Hellper - posté le 15/06/2013 à 21:48:55 (5402 messages postés) ❤ 0
Tonton Hellper	En fait la démonstration est pas compliquée à faire mais j'ai la flemme de la faire.
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux

Roi of the Suisse - posté le 15/06/2013 à 21:57:38 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	J'accepte la réponse d'hellper à la première question. C'est bel et bien 6. Pour la deuxième question, sa carte à 6 couleurs est correcte. Cependant, il y a une solution plus optimisée que sa carte, avec seulement 6 pays ! Et une démonstration rigoureuse est très compliquée. J'ai des pdf de 50 pages qui ne traitent que les cas à 5 couleurs.
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Kisthune - posté le 15/06/2013 à 22:01:43 (1227 messages postés) ❤ 0
Oui c'est fait à l'arrache	Doit y avoir un truc que j'ai pas saisi...
Reikon no Yume

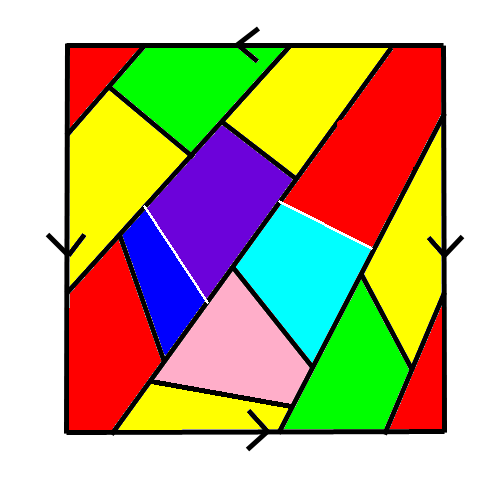
Tasslehoff - posté le 15/06/2013 à 22:03:18 (5274 messages postés) ❤ 0
Disciple de Pythagolf	Ta zone bleu marine et ta zone violette pourraient être de la même couleur. ET ta deuxième zone blanche peut être rose.
~~

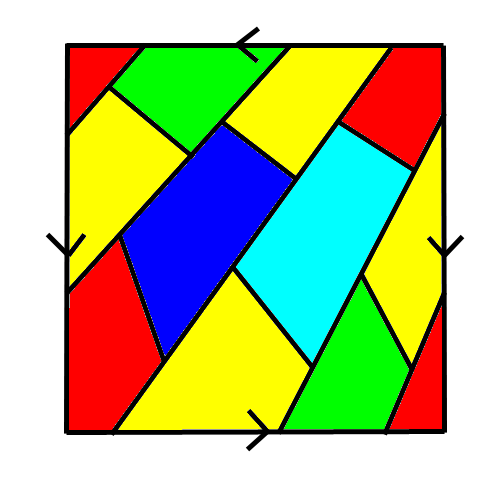
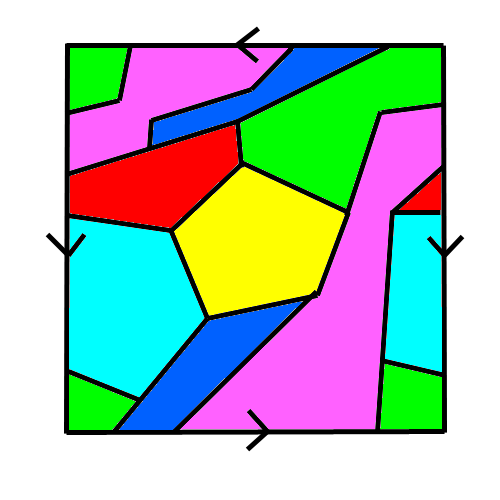
Roi of the Suisse - posté le 15/06/2013 à 22:04:06 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Quiche : tes deux pays bleus ne se touchent pas, ils peuvent avoir la même couleur du coup. Ce qui fait bel et bien 6 Personne pour la carte minimale ?
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Tasslehoff - posté le 15/06/2013 à 22:15:45 (5274 messages postés) ❤ 0
Disciple de Pythagolf	J'ai ça : ?
~~

Kisthune - posté le 15/06/2013 à 22:23:51 (1227 messages postés) ❤ 0
Oui c'est fait à l'arrache	Merci Rots, plus c'est évident et moins je le vois. Tasslehof : les lignes blanches ce sont des frontières. J'ai juste fait ça vraiment à l'arrache !
Reikon no Yume

Roi of the Suisse - posté le 15/06/2013 à 22:24:58 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Tass : oui ! Même si c'est très malpoli d'avoir mis la frontière orange-violet sur un côté du carré. Voici la mienne : C'est la carte des régions de Kujira. Je mets des petits clins d'oeils mathématiques, même si personne ne les verra jamais =>[] Bravo à Hellper pour avoir trouvé en premier une carte à 6 couleurs, et à Tasslehoff pour avoir trouvé la carte minimale !
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Tasslehoff - posté le 15/06/2013 à 22:29:29 (5274 messages postés) ❤ 0
Disciple de Pythagolf	\o/ Citation: Même si c'est très malpoli d'avoir mis la frontière orange-violet sur un côté du carré. Yé souis dézolé. Citation: Tasslehof : les lignes blanches ce sont des frontières. J'ai juste fait ça vraiment à l'arrache ! Ah j'ai cru que tu voulais faire voir ton coté antisocial en mettant des lignes comme zones.
~~

Roi of the Suisse - posté le 15/06/2013 à 22:39:58 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	À propos de l'énigme précédente : Cette énigme est basée sur la seule figure qui ne vérifie pas la version généralisée du théorème des quatre couleurs ! Le théorème des quatre couleurs dit que toute carte sur un plan peut être coloriée avec seulement 4 couleurs. Plus tard on a découvert que des cartes sur des surfaces bizarres demandaient plus de couleurs, c'est le cas du tore (bouée) qui nécessite jusqu'à 7 couleurs pour colorier certaines de ses cartes. Une formule permet de savoir combien de couleurs il faut au minimum pour colorier n'importe quelle carte d'une surface donnée : (7 + sqrt(49 - 24x))/2 où x est la caractéristique d'Euler de la surface. Cette formule a été démontrée par un ordinateur qui a traité tous les cas possibles, et ça lui a pris beaucoup beaucoup de temps. Une seule surface ne respecte pas cette formule : la bouteille de Klein, pour laquelle la formule prévoit 7 couleurs alors que 6 suffisent (Franklin l'a démontré en 1934). C'est cette figure qui était la planète de l'énigme. La bouteille de Klein n'a pas de plongement continu dans un espace à trois dimensions. Pour ne pas s'entrecouper elle-même, la planète de l'énigme doit donc se trouver dans un espace d'au minimum 4 dimensions. Énigme n° 156 : Comment découper un carré en 7 triangles de même aire ? Version vulgarisée de l'énigme : Lors d'un anniversaire, une mère doit partager équitablement un gâteau carré en 7 parts triangulaires pour chaque nenfant, quel découpage utiliser ? ça vous aidera peut-être plus =>[]
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Hellper - posté le 20/06/2013 à 16:06:52 (5402 messages postés) ❤ 0
Tonton Hellper	Ça compte si je fait 8 parts de gâteau et que j'en garde une pour moi ? Edit : Les parts doivent être entières ou peuvent être fragmentées ?
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux

Roi of the Suisse - posté le 20/06/2013 à 16:24:23 (30336 messages postés) - - ❤ 0
Chanter l'hyperchleuasme	Les parts sont en un seul morceau.
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte

Anton_ - posté le 20/06/2013 à 16:44:42 (1535 messages postés) ❤ 0
	Triangle de même aire ne veut pas forcément dire triangle égaux, ils partagent juste la même base et la même hauteur ... Bigre, un nombre impair... J'arrive pas à trouver... question pour matheux : Comment couper un disque en 3 parties équitables avec deux segments parallèles ?
Raetribution | Megamike || tutos : 1 2 || Une bonne dose de maths pour la route

Tasslehoff - posté le 20/06/2013 à 16:50:29 (5274 messages postés) ❤ 0
Disciple de Pythagolf	Citation: ils partagent juste la même base et la même hauteur Pas forcément, le résultat de la multiplication des deux doit être le même.
~~

Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

Index du forum > La Taverne > Topic des énigmes BDM