Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
 Provided by Weboo!
Provided by Weboo!
Reprise du message précédent:
Tasslehoff -
posté le 20/06/2013 à 16:50:29 (5275 messages postés)
| Disciple de Pythagolf | Citation: ils partagent juste la même base et la même hauteur |
Pas forcément, le résultat de la multiplication des deux doit être le même.
|
~~ |
Suite du sujet:
Kisthune -
posté le 20/06/2013 à 17:07:45 (1227 messages postés)
| Oui c'est fait à l'arrache | Le problème n'aurait pas été drôle avec des parts paires.
À quand des énigmes de français ?
|
Reikon no Yume |
|
| Chanter l'hyperchleuasme | Anton : C'est malpoli de poser une énigme alors qu'il y en a déjà une en cours 
Spoiler (cliquez pour afficher) 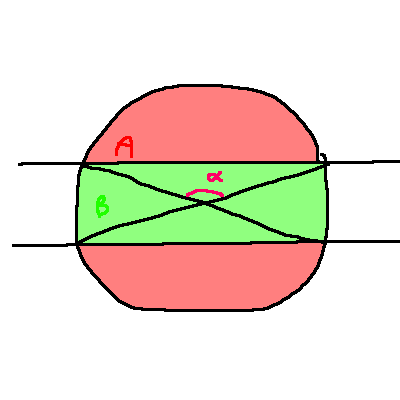
A1 = A2 = pi R² a/(2pi) - (R² sin a)/2
B = R² sin a + pi R² 2 (pi - a) / (2pi)
A1 = B
pi R² a/(2pi) - (R² sin a)/2 = R² sin a + pi R² 2 (pi - a) / (2pi)
pi a/(2pi) - (sin a) /2 = (sin a) + pi (1 - a/pi)
a/2 = (3/2) sin a + pi - a
a = sin a + (2/3) pi
Spoiler (cliquez pour afficher) Vu la figure, l'angle a fait un peu moins que pi. On pose x = pi - a :
pi/3 = x + sin x
pi/3 = 2x car x petit ctb
x = pi/6
a = pi - pi/6 a = 2,6 radians = 149°
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Anton_ -
posté le 20/06/2013 à 17:26:08 (1539 messages postés)
| | Désolé, je ne le ferai plus...
|
Raetribution | Megamike || tutos : 1 2 || Une bonne dose de maths pour la route |
klimero -
posté le 20/06/2013 à 17:30:18 (5372 messages postés)
| | J'aurais du plus bosser en maths cette année pour pouvoir répondre aux énigmes de rots :0
Une petite question : y'a-t-il plusieurs possibilités au final ou elles sont toutes construites sur le même modèle ?
|
Some pirates achieved immortality by great deeds of cruelty or derring-do. Some achieved immortality by amassing great wealth. But the captain had long ago decided that he would, on the whole, prefer to achieve immortality by not dying. |
|
| Chanter l'hyperchleuasme | Il n'y a qu'une possibilité (à des symétries/rotations près évidemment).
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
klimero -
posté le 20/06/2013 à 17:53:22 (5372 messages postés)
| | Est-ce que c'est grosso modo comme ça :
Spoiler (cliquez pour afficher)
C'est à dire en "tournant" de l’extérieur vers l'intérieur ?
(évidemment ici c'est faux au niveau aire des triangles etoo)
|
Some pirates achieved immortality by great deeds of cruelty or derring-do. Some achieved immortality by amassing great wealth. But the captain had long ago decided that he would, on the whole, prefer to achieve immortality by not dying. |
|
| Chanter l'hyperchleuasme | Bon, j'arrête de vous troller, c'est malhonnête de ma part : on ne peut pas 
C'est Hellper qui a bon :
Citation: Ça compte si je fait 8 parts de gâteau et que j'en garde une pour moi ? |
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tasslehoff -
posté le 20/06/2013 à 18:08:23 (5275 messages postés)
| Disciple de Pythagolf | J'avais pensé que c'était impossible, mais cette phrase :
Citation: Il n'y a qu'une possibilité (à des symétries/rotations près évidemment). |
M'a fait penser qu'il y avait un solution. C'est méchant. 
|
~~ |
|
| Chanter l'hyperchleuasme | Oui. Je me repens 
Faut rendre toutes les lignes vraies en utilisant les symboles listés en dessous :
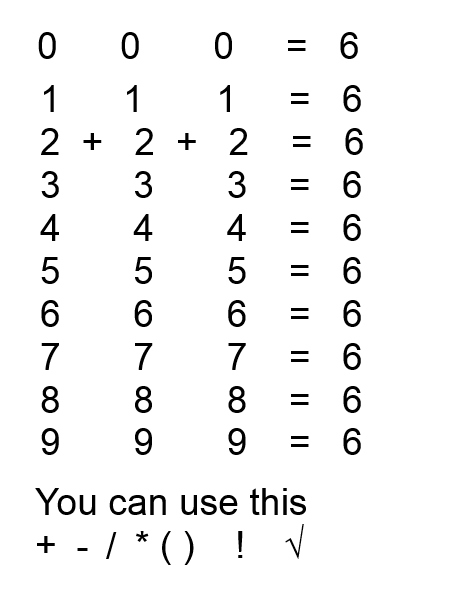
Il y a globalement deux méthodes.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
|
| Chanter l'hyperchleuasme | Pfff c'est juste des plusses et des fouahs 
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Anton_ -
posté le 28/07/2013 à 18:10:40 (1539 messages postés)
| | Pour les trois 8, je vois pas, mais pour tous les autres c'est easy.
Spoiler (cliquez pour afficher) factoriel de 8 = 5760 ... c'est trop grand pour en faire quelque chose.
8+8+8 = 24 = 3*6, zut, il manque une division par trois...
8-(8/8) = 7 ça marchait pour les 7, mais pas ici...
(8+8)/8 = 2 mince, si seulement j'avais un huit de plus
racine de huit ça donne 2^(3/2), bigre ça sert à rien.
eh mais ... 8+8 = 16 ...
V(V16) = 2
8 - V(V(8+8)) = 6
|
Raetribution | Megamike || tutos : 1 2 || Une bonne dose de maths pour la route |
Zeus81 -
posté le 28/07/2013 à 18:17:50 (11071 messages postés)
| | J'en ai trouvé un : 6 + 6 - 6 = 6

|
|
| Chanter l'hyperchleuasme | Anton : Bah donne-les tous alors.
Zeus : Bravo ! Il y avait aussi 6 * 6 / 6 = 6 
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
|
| Chanter l'hyperchleuasme | Heureusement qu'Anton était là pour le 8 
Voici la solution alternative :
Spoiler (cliquez pour afficher) 0 + 0 + 0 != 6
1 + 1 + 1 != 6
2 + 2 + 2 = 6
3 + 3 + 3 != 6
4 + 4 + 4 != 6
5 + 5 + 5 != 6
6 + 6 + 6 != 6
7 + 7 + 7 != 6
8 + 8 + 8 != 6
9 + 9 + 9 != 6

|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
2dt_ -
posté le 28/07/2013 à 18:38:41 (291 messages postés)
| | Solution :
Spoiler (cliquez pour afficher)
!( !0 + !0 + !0 ) = 6
! ( 1 + 1 + 1 ) = 6
2 + 2 + 2 = 6
3 * 3 - 3 = 6
V(4) + V(4) + V(4) = 6
5 + !(5-5) = 6
6 + 6 - 6 = 6
7 - !(7-7) = 6
8 - V( V(8+8)) = 6
V(9) * V(9) - V(9) = 6
combo grilled
|
|
| Chanter l'hyperchleuasme | Avec le 3 y'avait V(3)*V(3)+3 aussi.
Alors voici une énigme qui demande pas mal d'explications au début, mais la question à la fin est simple.
Ci-dessous, un noeud :
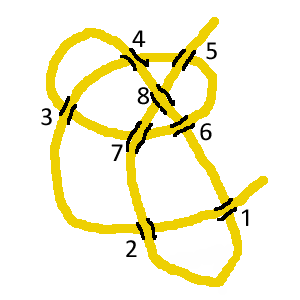
C'est une corde qui s'entrelace avec elle-même, je suppose que vous avez l'habitude de voir ce genre de choses dans vos câbles d'écouteurs.
Si on tire chacune des extrémités de la corde, un noeud se forme. C'est la galère pour le défaire.
Ci-dessous, un non-noeud :
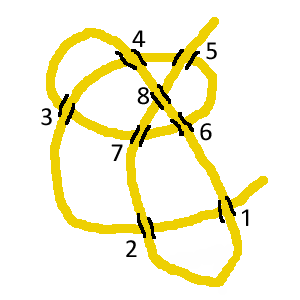
Il ressemble au précédent, mais si on regarde attentivement, on s'aperçoit qu'il ne s'agit que d'une boucle posée sur une autre boucle.
Si on tire la corde aux extrémités, il n'y a pas de noeud. C'est ce que les magiciens appellent un noeud magique je suppose.
Numérotons les croisements que fait la corde avec elle-même. Ici il y en a 8 à chaque fois.
Partons d'une extrémité, et listons les croisements rencontrés, dans l'ordre. On précise si on passe au dessus ou bien en dessous avec un + ou un -.
Pour les deux noeuds, les listes de croisements rencontrés sont :

+1 -2 +3 -4 -5 +6 -7 -3 +4 +8 -6 -1 +2 +7 -8 +5 pour le vrai noeud

-1 -2 +3 -4 -5 -6 -7 -3 +4 +8 +6 +1 +2 +7 -8 +5 pour le faux noeud
Vérifiez que je ne me suis pas trompé (et que vous avez compris la notation) en suivant la corde avec le doigt.
Maintenant, sur le bord d'un cercle, mettons dans l'ordre tous les croisements rencontrés ; puis relions les croisements de même numéro (qui sont le même croisement, une fois passé par au dessus, une fois passé par en dessous) :
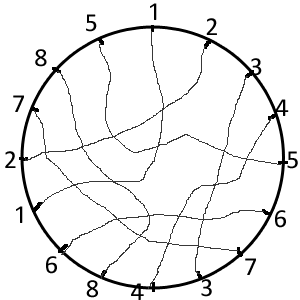
Pour préciser dans quel sens se fait le croisement, on met le long des lignes des petites flèches allant du passage sous le croisement au passage sur le croisement :

pour le vrai noeud (+1 -2 +3 -4 -5 +6 -7 -3 +4 +8 -6 -1 +2 +7 -8 +5)
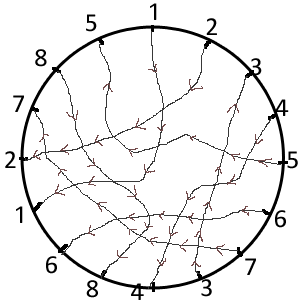
pour le faux noeud (-1 -2 +3 -4 -5 -6 -7 -3 +4 +8 +6 +1 +2 +7 -8 +5)
Les flèches vont du - vers le +.
Maintenant, on va tracer une "constellation" pour chacun de ces filets...
Chaque maille du filet possède des flèches sur son pourtour. Interessons nous aux coins des mailles et au comportement des flèches dans ces coins :
- parfois, un coin de la maille se fait pointer par deux flèches (----->-----coin-----<-----)
- parfois un coin de la maille se fait fuir par les deux flèches (-----<----coin----->-----)
C'est à ces deux types de coins qu'on va s'intéresser : les coins attirants et les coins repoussants.
Le troisième type de coin, où les flèches ne font que passer, ne nous intéresse pas (---->----coin---->----).
Quand deux lignes se croisent et forment un coin attirant, il y a un coin repoussant de l'autre côté du point de croisement.
Un croisement de lignes qui comporte un coin attirant et un coin repoussant constitue une "porte" d'une maille à une autre. On marque les deux mailles par un gros point rouge, et on relie les deux points rouges par un trait qui traverse la porte, c'est-à-dire le coin repoussant et le coin attirant.
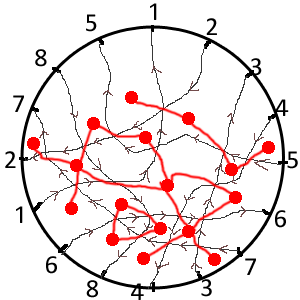
pour le vrai noeud
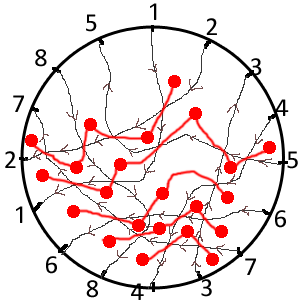
pour le faux noeud
Comprenez bien comment j'ai construit ces constellations en fonction de la nature des coins des mailles des filets.
Maintenant une observation de ces constellations :
- Le vrai noeud a une constellation qui comporte des cycles (la ligne rouge forme des carrés, des triangles...) et des carrefours (sur certains points rouges, il y a plus de deux chemins rouges qui partent).
- Le faux noeud a une constellation qui ne comporte que des lignes ! Pas de cycles, pas de carrefours.
Coïncidence ?
Question de l'énigme :
Trouvez un vrai noeud dont la constellation ne comporte ni cycle ni carrefour, ou bien un faux noeud dont la constellation comporte un cycle ou un carrefour.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Hellper -
posté le 09/09/2013 à 16:02:48 (5402 messages postés)
| Tonton Hellper | Je dis que c'est impossible. Mais j'ai la flemme de la prouver alors si vous n'êtes pes contents c'est que j'ai raizon et vous avez tord.
|
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux |
|
| Chanter l'hyperchleuasme | C'est possible 
Trouver un non-noeud dont la constellation fait des cycles/carrefours est plus simple que trouver un vrai noeud à constellation linéaire cela dit...
Pour prouver mon honnêteté, voici un non-noeud dont la constellation contient des cycles :
N = +1-2+3+4-5-6+7-8+9-10-4+11-12+5+13-9-14-3+15-1+8-7+6-13+10+14+2-15-11+12
Les plus perspicaces auront bien sûr reconnu le noeud de Thistlethwaite 
Spoiler (cliquez pour afficher) Bon, même en dessinant le noeud, on a du mal à bien se rendre compte que c'est un non-noeud, alors voici la preuve que c'est bien un non-noeud :
N = +1-2+3+4-5-6+7-8+9-10-4+11-12+5+13-9-14-3+15-1+8-7+6-13+10+14+2-15-11+12
On remarque dans l'écriture un cycle de jumeaux :
N = +1-2(+3+4)-5-6+7-8+9(-10-4)+11-12+5+13-9(-14-3)+15-1+8-7+6-13(+10+14)+2-15-11+12
Le cycle est (+3+4) (-4-10) (+10+14) (-13-3) (+3+4). On peut le supprimer, c'est comme des dominos.
N = +1-2-5-6+7-8+9+11-12+5+13-9+15-1+8-7+6-13+2-15-11+12
En regardant vite fait, on ne voit plus trop de cycle de jumeaux...
On peut faire une inversion de triplet en vertu du troisième mouvement de Reidemaster :
N = +1-2(-5-6)+7-8+9+11-12(+5+13)-9+15-1+8-7(+6-13)+2-15-11+12
On fait passer la ficelle (+5+13) au dessus du croisement 6, ce qui a pour effet d'inverser les trois couples :
N = +1-2(-6-5)+7-8+9+11-12(+13+5)-9+15-1+8-7(-13+6)+2-15-11+12
N = +1-2-6-5+7-8+9+11-12+13+5-9+15-1+8-7-13+6+2-15-11+12
On remarque alors un petit cycle de jumeaux :
N = +1(-2-6)-5+7-8+9+11-12+13+5-9+15-1+8-7-13(+6+2)-15-11+12
Le cycle est (-2-6) (+6+2) (-2-6). C'est comme les dominos, ça s'en va.
N = +1-5+7-8+9+11-12+13+5-9+15-1+8-7-13-15-11+12
Bon, je sais pas trop quoi faire alors je vous propose une inversion du triplet 11 15 9 grâce au troisième mouvement de Reidemaster, on verra bien...
N = +1-5+7-8(+9+11)-12+13+5(-9+15)-1+8-7-13(-15-11)+12
La ficelle (+9+11) passe au dessus du croisement 15, et inverse les trois couples :
N = +1-5+7-8(+11+9)-12+13+5(+15-9)-1+8-7-13(-11-15)+12
Hum, que pouvons nous faire...
N = +1-5+7-8+11+9-12+13+5+15-9-1+8-7-13-11-15+12
Je propose encore une inversion de triplet avec 7 13 5 :
N = +1(-5+7)-8+11+9-12(+13+5)+15-9-1+8(-7-13)-11-15+12
N = +1(+7-5)-8+11+9-12(+5+13)+15-9-1+8(-13-7)-11-15+12
On a ça :
N = +1+7-5-8+11+9-12+5+13+15-9-1+8-13-7-11-15+12
C'est assez cool, parce qu'on voit un cycle de jumeaux :
N = (+1+7)-5-8(+11+9)-12+5+13+15(-9-1)+8-13(-7-11)-15+12
Le cycle est (+1+7) (-7-11) (+11+9) (-9-1) (+1+7), ça disparait comme des dominos.
N = -5-8-12+5+13+15+8-13-15+12
On remarque un nouveau cycle de jumeaux : (+13+15) (-13-15) (+13+15)
N = -5-8-12+5(+13+15)+8(-13-15)+12
N = -5-8-12+5+8+12
Et encore un : (-5-8) (+5+8) (-5-8)
N = (-5-8)-12(+5+8)+12
N = -12+12
On tombe alors sur une bête boucle simple.
N = 0
Donc le noeud est bien un non-noeud 
Mais il y a des non-noeuds à constellation cyclique beaucoup plus simples que celui-là.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
|
| Chanter l'hyperchleuasme | C'est pas des maths, c'est que du dessin de schémas et un peu d'imagination 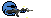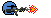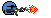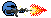
EDIT :
Une solution beaucoup plus simple !
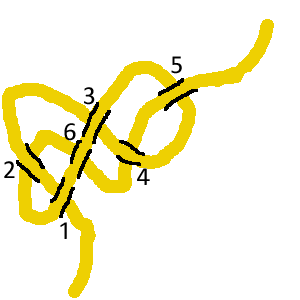
N = -1+2-3+4-5+3+6+1-2-6-4+5
On fait passer la ficelle (-6-4) en dessous du croisement 3 :
N = -1+2(-3+4)-5(+3+6)+1-2(-6-4)+5
N = -1+2(+4-3)-5(+6+3)+1-2(-4-6)+5
N = -1+2+4-3-5+6+3+1-2-4-6+5
On enlève le cycle (+2+4) (-2-4) :
N = -1(+2+4)-3-5+6+3+1(-2-4)-6+5
N = -1-3-5+6+3+1-6+5
On enlève le cycle (-1-3) (+3+1) :
N = (-1-3)-5+6(+3+1)-6+5
N = -5+6-6+5
On défait la boucle 6 :
N = -5(+6-6)+5
N = -5+5
On défait la boucle 5 :
N = (-5+5)
N = 0
C'est bien un noeud magique.
Pourtant sa constellation comporte deux cycles et un carrefour :
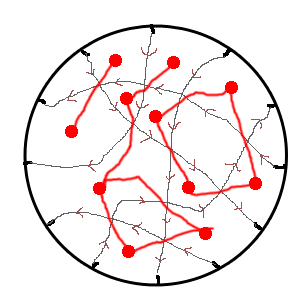
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Hellper -
posté le 07/11/2013 à 21:35:15 (5402 messages postés)
| Tonton Hellper | Je me permet de ranimer le topic avec une petite énigme :
Nous allons considérer un certain type de nombre que nous appellerons les nombres rouge selon la définition :
Citation: Un nombre rouge est un nombre non palindromatique dont le renversement de son carré est égal au carré de son renversement |
Pour illustrer cette définitions voici un exemple, 13
Si on met 13 au carré on obtient 169
Si on renverse 169 on obtient 961
Si on renverse 13 on obtient 31
Si on met 31 au carré on obtient 961
On peut essayer la même chose avec d'autres nombres comme 12, 103, 112 ...
Maintenant que vous voyez ce qu'est un nombre rouge, voici ma question :
Existe-t-il un nombre fini de nombres rouges ? Si oui, combien y en a-t-il ?
|
La liste des raisons pour lesquelles le making se meurt, la cinquième va vous étoner | Des projets abandonnés, source d'inspiration :D | Mes jeux |
|
| Chanter l'hyperchleuasme | Y'a tous les nombres du type 1000...0002 qui sont valides déjà (leur carré est 1000...0004000...0004), donc une infinité 
Pareil pour 1000...0003 (de carré 1000...0006000...0009) donc disons deux infinités.
|
Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte |
Tassle -
posté le 08/11/2013 à 02:22:15 (5275 messages postés)
| Disciple de Pythagolf | Et dans une base n>4 ça devrait marcher avec n^k+m, m étant supérieur ou égal à 2 et strictement inférieur à racine de n (avec k un entier naturel non nul).
Enfin je crois. 
|
~~ | Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27Index du forum > La Taverne > Topic des énigmes BDM



|

 Chat
Chat





















 -
- 







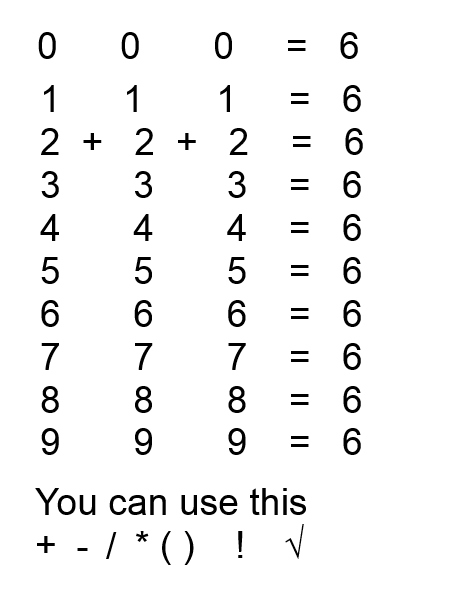





 .
.