❤ 0 EMG 7 : La récursivité
I Introduction
Ce tutoriel fonctionne pour tous les RM.
Si c'est le premier tutoriel de la série que vous lisez, je vous conseille fortement de lire les précédents qui sont des aides à la compréhension de ce tutoriel.
II Concept
La récursivité désigne un morceau de code qui fait référence à lui même, que ce soit directement dans lui-même ou par un autre morceau de code qu'il appelle (aka le premier exécute le seconde qui exécute le premier). Cette technique est souvent opposée à la méthode itérative qui préférera jouer sur les effets de bord là ou la récursivité se base plutôt sur le retour de valeur.
III Exemple
Pour donner un exemple, reprenons le code du premier tuto sur le calcul de puissance :
1
2
3
4
5
6
7
8
9
10
11
12
| def power(nombre, puissance)
accumulateur = 1
while true
if puissance == 0
break
end
accumulateur *= nombre
puissance -= 1
end
return accumulateur
end
puts power(2, 3) |
Ici il s'agit d'une méthode itérative car non seulement il n'y a pas appel de la fonction dans son propre corps mais en plus on utilise la variable puissance pour compter le nombre de fois que la boucle va s'effectuer (on réduis sa valeur petit à petit et une fois qu'elle atteint 0, on quitte la boucle).
Voici maintenant son équivalent récursif :
1
2
3
4
5
6
7
| def power(nombre, puissance)
if puissance == 0
return 1
else
return nombre * power(nombre, puissance - 1)
end
puts power(2, 3) |
On remarque alors que le code est plus court, pour un même calcul (même s'il faut garder en tête que les deux versions n'ont pas été compactées le plus possible).
Je ne pense pas avoir à vous expliquer le fonctionnement de la méthode itérative. penchons-nous cependant sur la méthode récursive.
Admettons que je veuille calculer 2**5 (aka deux à la puissance cinq). Ce qu'on sait c'est qu'on peut remplacer cette écriture par celle-ci :
2*2*2*2*2 avec autant de 2 que que le nombre de la puissance (ici 5). Hors en modifiant légèrement ce calcul on peut obtenir ceci :
2*(2*2*2*2) dont on remarque que le calcul entre parenthèses n'est autre que la définition de 2**4. Et on peut répéter le processus ainsi pour constater que 2**4 c'est 2*(2**3) :
2*(2*(2*(2*(2*(1))))
De fait, il est possible de généraliser le calcule de la puissance comme ceci :
Pour tout x :
x ** 0 vaut 1
x ** n vaut n * (x ** (n-1))
On peut constater d'ailleurs qu'un définition récursive possèdes au moins deux cas différents à gérer : Le cas avec n pour l'appel récursif et le cas avec 0 pour stopper la boucle récursive
Enfin bon c'est beau tout ça mais il faudrait voir ce que ça donne en event.
IV En event
Si la récursivité peut-être intéressante, elle a malheureusement besoin de variables locales pour être utilisées. En effet, si on reprend l'exemple dessus pour calculer 2**5 il faut qu'il calcule au préalable 2**4 pour le multiplier par 2, ce qui implique de calculer 2**3 pour aussi le multiplier par 2, etc...
Ce que va donc faire l'ordinateur c'est lancer le calcul de 2**5 qui va lancer le calcul de 2**4 qui va lancer le calcul de 2**3 qui va... lancer le calcul de 2**0. Ce dernier calcul va alors retourner 1 qui va être récupéré par le calcul de 2**1 pour le multiplier par 2 et le retourner puis 2**2 va effectuer la même chose à ce retour et ainsi de suite jusqu'à ce que la fonction qui calcule 2**5 retourne le bon résultat.
Ce qu'il faut retenir de ceci, c'est qu'à un moment, tous les calculs de puissances invoqués sont présents en mémoire au même moment. Il est donc indispensable que les variables nombre et puissance soient locales à la fonction qui les utilise pour ne pas avoir des collisions.
De fait, est-il possible de reproduire cette fonction dans RM ? Non. Mais il est possible de contourner le problème.
En effet, comme les events communs n'ont ni paramètres ni retour le seulement moyen d'aborder le problème est de passer par les effets de bord. Ainsi voici une solution au problème :
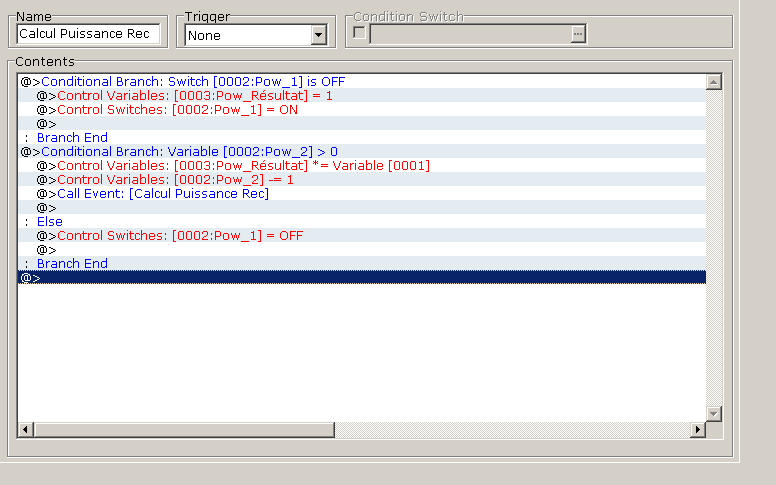
En fait ce que fait ce code c'est :
Le première condition vérifie que c'est la première execution du programme et si ce cas initialise une variable en la mettant à 1.
Et la seconde condition regarde s'il y a encore besoin de multiplier le résultat et d'appeler l'event commun. Si ce n'est pas l'interrupteur est désactivé et on sort de la boucle récursive.
Pour faciliter la comparaison, voici la version itérative utilisée dans le premier tuto :
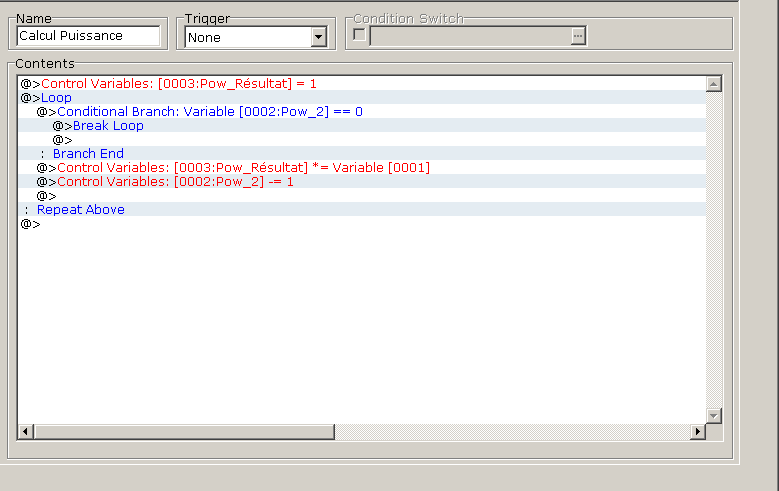
On se rend compte que le code itératif est actuellement plus compact, mais il serait en fait possible de raccourcir le code récursif en appelant un premiert event commun qui initialise le résultat à 1 et qui en appelle un second faisant le calcul récursif. De fait il n'y aurait plus besoin de conditions utilisant l'interrupteur.
Aussi, le code peut, quand il n'utilise pas plus de variables que ses arguments devenir plus compact, en atteste ce code qui réimplémente le modulo :
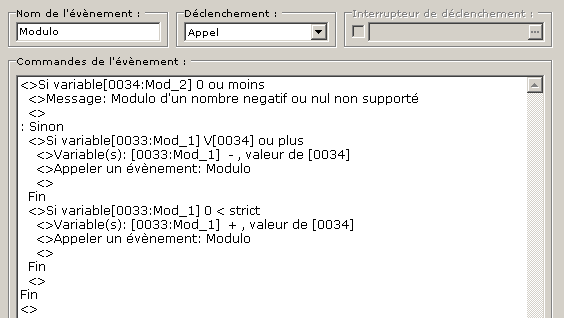
Et je pense qu'il sera plus facile de vous expliquer le fonctionnement avec cet event là.
En fait ce qu'il faut comprendre c'est qu'un event commun n'est finalement qu'une séquence d'instructions mire de côté pour pouvoir être exécutée à la demande. De fait dans notre cas si on voulait utiliser cet event commun pour calculer 11 % 2 il se passerait :
- 11 est supérieur ou égal à 2 ? Oui
- On lui retranche 2 -> il reste 9
- On appelle l'event commun qui va refaire ce qui a été fait jusque là mais avec 9
- 9 est supérieur ou égal à 2 ? Oui
- On lui retranche 2 -> il reste 7
- On appelle l'event commun qui va refaire ce qui a été fait jusque là mais avec 7
- 7 est supérieur ou égal à 2 ? Oui
- On lui retranche 2 -> il reste 5
- On appelle l'event commun qui va refaire ce qui a été fait jusque là mais avec 5
- 5 est supérieur ou égal à 2 ? Oui
- On lui retranche 2 -> il reste 3
- On appelle l'event commun qui va refaire ce qui a été fait jusque là mais avec 3
- 3 est supérieur ou égal à 2 ? Oui
- On lui retranche 2 -> il reste 1
- On appelle l'event commun qui va refaire ce qui a été fait jusque là mais avec 1
- 1 est supérieur ou égal à 2 ? Non
- Il ne reste plus rien à faire et les events communs s'arrêtent
On constate donc bien que 11 % 2 = 1
V Conclusion
Dans ce tuto nous avons pu aborder la récursivité, un concept fort de la programmation qui peut être simulé (même si c'est un peu maladroit) dans des events communs.
Cela ne vous servira pas dans toutes les situations mais je pense qu'il existe de nombreux cas comme le calcul du modulo qui peuvent se révéler intéressants, ne serait-ce que pour le plaisir de programmer autrement !
| 
 Chat
Chat