❤ 1Roi of the Suisse Quelques tests géométriques simples
Dans ce tuto je vais vous montrer comment tester certaines propriétés géométriques simples en 2D, du style « Est-ce que tel point est à une distance inférieure à d de tel droite ? » ou « Est-ce que tel point est à l’intérieur de tel triangle ? ». Je vais essayer d'illustrer chaque test avec un exemple d’application possible pour un jeu vidéo, mais il se peut que le test vous soit utile dans un tout autre contexte. Ce tuto donne des outils plutôt que des produits finis.
Tous les tests sont basés sur l’addition, la soustraction, la multiplication et la comparaison de nombres entiers uniquement (tant que les objets manipulés ont des coordonnées entières). Ils peuvent donc être utilisés dans beaucoup de logiciels différents, sont précis et relativement peu coûteux en termes de ressources de l’ordinateur.
NOTE :
Dans tout ce qui suit, je vais partir du principe que les axes du système de coordonnées sont tels que l’axe des y pointe d’un quart de tours plus loin que l’axe des y dans le sens anti-horaire (sens inverse des aiguilles d’une montre). Par exemple si l’axe des x pointe vers la droite, l’axe des y pointe vers le haut. Si l’axe des x pointe vers le haut, l’axe des y pointe vers la gauche. Et ainsi de suite.
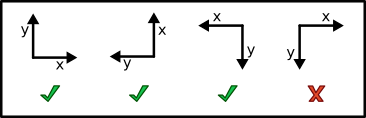
Illustrations de quelques systèmes de coordonnées valables et un qui ne l’est pas.
Si le système de coordonnées dans votre logiciel est dans « le mauvais sens », pas de panique. La seule différence se situe au test 2 de ce tuto, où je préciserai ce qu'il faut changer.
NOTATIONS :
• J’utilise le point central ⋅ pour dénoter la multiplication.
• Pour un point dans le plan P, je note ses coordonnées xP et yP (c’est pas beau mais faire beaucoup mieux sur un forum pas adapté à ce genre de choses). J’ecrirai aussi P = (xP,yP).
• Si P et Q sont deux points différents, je note (P,Q) la droite qui passe par P et Q et je note [P,Q] le segment de droite qui va de P à Q.

SOMMAIRE
• TEST 1 : Tester la distance entre deux points
• TEST 2 : Tester l’orientation de trois points
• TEST 3 : Tester si deux segments s’intersectent
• TEST 4 : Tester la distance d’un point à une droite
• TEST 5 : Tester la distance d’un point à un segment
• TEST 6 : Tester si un point est dans un polygone convexe
• TEST 7 : Tester l’appartenance à un polygone général

TEST 1 : Tester la distance entre deux points
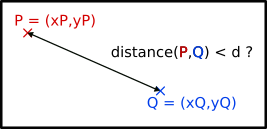
Bon, celui là est facile et la plupart d’entre vous savent probablement déjà comment faire. Disons que j’ai deux points P et Q de coordonnées respective (xP,yP) et (xQ,yQ).
Leur distance est : sqrt((xP-xQ)² + (yP-yQ)²), où sqrt désigne la fonction « racine carrée » (« square root » en anglais). Donc pour tester si les deux points sont à distance moins de d, il suffit de regarder si
sqrt((xP-xQ)² + (yP-yQ)²) < d ?
Sauf que je vous avais promis d’utiliser que des nombres entiers et les operations arithmétiques de base. Donc on va passer le tout au carré pour nous débarasser de cette méchante racine, ce qui donne le test :
(xP-xQ)² + (yP-yQ)² < d² ?
Application :
Les application sont innombrables, et je suis sûr que vous pouvez en trouver plein par vous-même. Pour donner un exemple, ça peut servir à tester si un ennemi est assez proche du héros pour le détecter et commencer à l’attaquer.

TEST 2 : Tester l’orientation de trois points
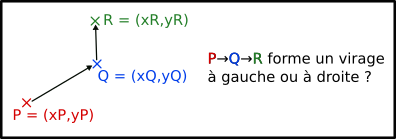
Ce test là est moins connu mais étonnamment utile. On a trois points P,Q et R et on veut savoir si le chemin qui va de P à Q puis de Q à R forme un virage à gauche ou à droite.
Pour ce faire, il suffit de tester le signe de :
Orientation(P,Q,R) = (xQ-xR)⋅(yR-yQ)-(yQ-yR)⋅(xR-xQ).
Si le système de coordonnées est « dans le mauvais sens » (voir l'intro du tuto) il faut multiplier par -1 et la formule devient :
Orientation(P,Q,R) = (yQ-yR)⋅(xR-xQ)-(xQ-xR)⋅(yR-yQ).
• Si Orientation(P,Q,R) = 0 alors les trois points P,Q et R sont alignés (donc soit la trajectoire P→Q→R va tout droit soit elle fait un demi tour complet arrivé à Q)
• Si Orientation(P,Q,R) > 0 alors la trajectoire P→Q→R forme un virage à gauche.
• Si Orientation(P,Q,R) < 0 alors la trajectoire P→Q→R forme un virage à droite.
Application :
Ça peut par exemple servir pour déterminer le message d’un copilote dans un jeu de course (« Attention, virage à gauche imminent ») ou pour savoir si un personnage a franchi une certaine ligne (Si P→Q→R forme un virage à gauche alors R se trouve à gauche de la droite orientée passant par P puis R. Si P→Q→R forme un virage à droite alors R se trouve de l’autre côté de cette droite).
On va également utiliser ce test comme une étape dans certains des tests suivants.

TEST 3 : Tester si deux segments s’intersectent
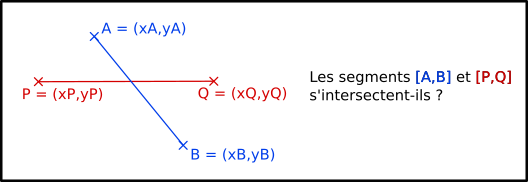
Disons qu’on a deux segments, le premier est [A,B] qui va du point A au point B et le second est [P,Q] (oui PQ caca c’est rigoulo) qui va du point P au point Q. On veut savoir si les deux s’intersectent.
Remarquez que si les deux segments s’intersectent, alors P et Q sont sur différents côtés de la droite passant par A et B. De même, A et B sont de côtés différents de la droite passant par P et Q. Inversement si ces deux conditions sont réunies, alors les deux segments s’intersectent.
Donc il suffit de tester ces orientations pour voir si les segments s’intersectent ! (voir le point 2 du tuto)
Bon j’ai passé sous silence le cas particulier où les deux segments sont alignés sur la même droite et tous les tests d’orientation vont donner 0. Ce cas est traité dans la première partie de la procédure qui suit.
Si Orientation(A,B,P) = 0 et Orientation(A,B,P) = 0 alors les deux segments sont alignés.
Dans ce cas les deux segments s'intersectent si et seulement si maximum(xA,xB) >= minimum(xP,xQ) et minimum(xA,xB) <= maximum(xP,xQ) et maximum(yA,yB) >= minimum(yP,yQ) et minimum(yA,yB) <= maximum(yP,yQ).
Si les segments ne sont pas alignés, alors ils s'intersectent si et seulement si Orientation(A,B,P)⋅Orientation(A,B,P) <= 0 et Orientation(P,Q,A)⋅Orientation(P,Q,B) <= 0.
Application :
Ce test est surtout utile pour des tests de collisions entre objets, qui peuvent être représentés par un segment ou par plusieurs (par exemple un rectangle composé de quatre segments).

TEST 4 : Tester la distance d’un point à une droite
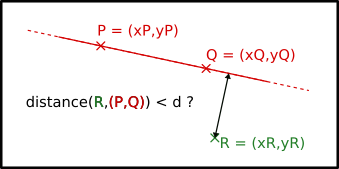
On a une droite D = (P,Q) qui passe par les points P et Q ainsi qu’un troisième point R. On veut savoir si la distance de R à D est inférieure à d.
Pour cela il suffit de tester si :
((xQ-xP) ⋅(yR-yP) - (yQ-yP)⋅(xR-xP))² < d²⋅((xQ-xP)²+(yQ-yP)²)
Application :
Ça peut servir à tester si un objet est trop près d’un mur par exemple, pour savoir si il peut continuer sa trajectoire ou si il faut le faire rebondir contre celui-ci. On peut aussi imaginer que la droite représente le rempart d’un château et que le point R représente le héros. S'il s’approche trop près du rempart, il se fait repérer/canarder/saluer.

TEST 5 : Tester la distance d’un point à un segment
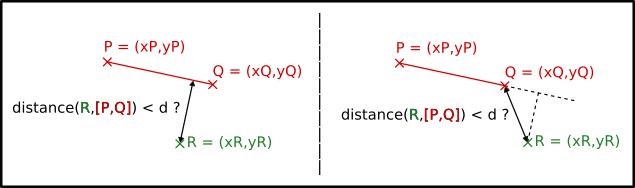
On a un segment S = [P,Q] qui va du point P au point Q ainsi qu’un troisième point R. On veut savoir si la distance de R à S est inférieure à d. C’est en quelque sorte un raffinement du test précédent, sauf qu’il faut également gérer le cas où la projection orthogonale de R sur la droite (P,Q) n’est pas sur le segment S (le cas de droite sur l’illustration précédente).
Pour ce faire on peut définir les points P’ = (xP – yQ + yP, yP + xQ – xP) et Q’ = (xQ – yQ + yP, yQ + xQ – xP).
Si Orientation(P,P’,R)⋅Orientation(Q,Q’,R) ≥ 0 alors on est dans le cas de droite sur la figure précédente. Pour savoir si la distance de R à [P,Q] est inférieure à d, il suffit de tester si la distance de R à P est inférieure à d ou si la distance de R à Q est inférieure à d (voir le test 1 de ce tuto). Je précise qu’il faut bien effectuer les deux tests (pour P et pour Q) et qu’il suffit que l’un des deux soit à distance inférieure à d pour que la distance de R à [P,Q] soit inférieure à d.
Si Orientation(P,P’,R)⋅Orientation(Q,Q’,R) < 0 alors on est dans le cas de gauche sur la figure précédente. Dans ce cas il suffit de tester si la distance entre R et la droite passant par P et Q est inférieure à d (voir le test 4 de ce tuto).
Application :
Globalement les applications sont similaire au test précédent, dans le cas où l’objet considéré (un mur par exemple) n’est pas de longueur infinie.

TEST 6 : Tester si un point est dans un polygone convexe
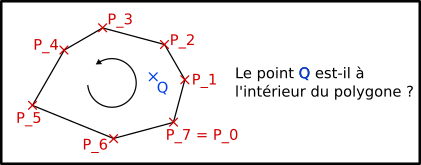
On a un polygone convexe défini par une suite de points P_1, P_2, …, P_(n-1) et P_n qui sont listés dans l'ordre obtenu en faisant le tour du polygone dans le sens anti-horaire. Parce que ça simplifiera les choses plus loin, on va aussi donner le nom P_0 au point P_n (c'est cohérent avec le fait qu'un polygone se « referme sur lui même », c'est à dire que si on fait le tour on commence et on finit au même point).
Convexe signifie qu’il n’y a pas d’angles « vers l’intérieur », pas de creux en quelque sorte (voir l’illustration du test suivant pour un polygone qui n’est pas convexe).
On a aussi un autre point Q et on veut tester si Q est à l’intérieur du polygone.
Pour ce faire, il suffit de tester si P_0→P_1→Q forme un virage à gauche et P_1→P_2→Q forme un virage à gauche et P_2→P_3→Q forme un virage à gauche, et ainsi de suite jusqu'à P_(n-1)→P_n→Q (voir le point 2 de ce tuto pour tester le sens d'un virage).
Si tous ces virages sont à gauche, Q est dans le polygone. Il suffit qu’un seul de ces virages soit vers la droite pour être sûr que Q n’est pas dans le polygone.
Quand un virage est plat (les points sont alignés) c’est à vous de décider si vous voulez le considérer comme un virage à gauche ou à droite, selon si vous voulez inclure les points sur le bord du polygone comme étant dans le polygone ou pas.
Application :
Tester si un personnage est dans une certaine zone. La zone en question peut même se déplacer si vous voulez. Un exemple que je trouve sympa est un triangle formé par trois ennemis, et on veut tester si le héros se trouve dans ce triangle (auquel cas il est considéré comme entouré d’ennemis et obtient un boost d’adrénaline ou un truc du genre).
Remarques :
Quand le polygone convexe en question est très grand (c'est à dire défini par beaucoup de points) il est possible d’accélérer beaucoup cet algorithme en utilisant ce qu’on appelle une recherche par dichotomie. Mais c’est un peu trop long à expliquer pour ce tuto.
Néanmoins, un moyen simple de souvent accélérer le test quand le polygone en question ne bouge pas est de commencer par tester si le point Q est au moins dans un « rectangle limite », qui contient le polygone.
On commence par calculer une fois pour toute xMin qui est le minimum de xP_1, xP_2,... xP_n, et aussi xMax qui est le maximum de xP_1, xP_2,... xP_n, et de même pour yMin et yMax. Quand je dis « une fois pour toute » je veux dire qu'il n'est pas nécessaire de recalculer ces valeurs à chaque test qu'on fait vu qu'elles vont rester les mêmes.
Puis, avant de tester si Q est dans le polygone, on commence par tester si xMin ≤ xQ ≤ xMax et yMin ≤ yQ ≤ yMax. Si ce n'est pas le cas, on sait d'avance que Q n'est pas dans le polygone et ce n'est pas la peine d'effectuer le test complet.

TEST 7 : Tester l’appartenance à un polygone général
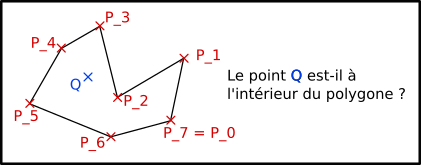
Cette question est similaire à la précédente mais dans le cas où le polygone n’est pas forcément convexe. Le test est basé sur l'idée que si on commence au point Q et qu'on avance dans une direction (disons vers la droite), on va passer par dessus le bord du polygone un certain nombre de fois. Si ce nombre est impair, Q est à l’intérieur du polygone. Si ce nombre est pair, Q est à l’extérieur du polygone.
En exploitant cette idée on peut arriver au test suivant :
On commence par définir w = 0.
Pour chaque i compris entre 0 et n-1 on fait ce qui suit (notez l'utilisation des inégalités strictes et larges, c'est pas fait au hasard et c'est important) :
SI yP_i < yQ ≤ yP_(i+1) ou bien yP_i ≥ yQ > yP_(i+1) alors :
SI (Orientation(P_i,P_(i+1),Q) > 0 et yP_(i+1) > yP_i) ou bien (Orientation(P_i,P_(i+1),Q) < 0 et yP_(i+1) < yP_i) alors :
w = 1-w
Fin SI
Fin SI
À la fin de cette procédure, w représente le résultat du test (si w = 1 alors Q est dans le polygone et si w = 0 alors Q n'est pas dans le polygone).
Si Q est exactement sur le bord du polygone alors la valeur de w dépend de la nature du bord en question, mais en pratique osef un peu si le test se trompe dans ce cas (à l’œil nu ça change rien si le bord fait partie de l'intérieur ou pas).
Remarques :
La même remarque sur le « rectangle limite » que dans le test précédent est valable ici.

Si vous avez des questions sur ces tests ou même sur comment tester d'autres propriétés géométriques qui n’apparaissent pas dans ce tuto n'hésitez pas à m'envoyer un MP (je risque de ne pas le voir si vous laissez seulement un commentaire ici). Je partagerai les réponses éventuelles dans les commentaires ci-dessous. La géométrie algorithmique étant mon domaine de prédilection, je serais ravi de pouvoir me rendre utile sur ça [img]smileys/sourire.gif" alt=" " /> " />
Ciao !
|

 Chat
Chat




























 " />
" />


 -
- 







